Eigenschappen van een lineair regressiemodel
Schatten van lineaire regressie
Eén van de belangrijste evaluatiecriteria bij een lineair regressiemodel is de meerwaarde van \(X\) in het verklaren van \(Y\). Indien we geen informatie zouden hebben over leeftijd en geslacht, kunnen we \(Y\) het best beschrijven aan de hand van het gemiddelde \(\bar{Y}\).
Om de waarde van de \(X\) variabele in te schatten in het verklaren van \(Y\), kijken we naar de afstand tussen de geschatte regressielijn en de observaties (punten op de grafiek). Wanneer de punten dichter tegen de lijn liggen in vergelijking met een schatting op basis van het algemene gemiddelde \(\bar{Y}\), dan lijkt het dat \(X\) een deel van \(Y\) lijkt te verklaren. Wanneer we \(Y\) willen schatten op basis van de regressielijn, dan duiden we deze schatting aan met \(\hat{Y}\). Zo zal voor \(X = 30\) jaar, \(\hat{Y} = 13.6 + (-0.2)30 = 7.6\).
Het verklaarde deel wordt uitgedrukt als verklaarde variantie. Het becijferen van deze verklaarde variantie gebeurt aan de hand van ANOVA tabellen. Zoals weergegeven in figuur 3.1 varieert \(Y\) over verschillende waarden. De blauwe bollen geven de observaties weer, terwijl de blauwe horizontale lijn het gemiddelde van \(Y\) weergeeft. De afstand van een observatie (blauwe bol) tot de horizontale lijn, maakt onderdeel uit van de totale variantie. Deze totale variantie wordt ook wel de kwadratensom (Sum of Squares) genoemd. Wiskundig wordt de totale spreiding gedefinieerd als de Total Sum of Squares (SST) ofwel \(\sum ({Y}_i - \bar{Y})^2\). Deze formule geeft aan dat het de som van alle afstanden betreft tussen de blauwe bollen en de blauwe horizontale lijn. Daarnaast hebben we ook de regressielijn of best passende rechte. De afstand van de blauwe bollen tot deze lijn, noemen we de resterende fout van het model of residu (SSE) wat wiskundig \(\sum ({Y}_i - \hat{Y})^2\) word ofwel het verschiul tussen de blauwe bollen en de regressielijn. Tot slot hebben we de verklaarde variantie van het model, welke uitdruk in welke mate het model meer verklaard van de variantie van \(Y\) t.o.v. \(\bar{Y}\). Dit wordt weergegeven door \(\sum (\hat{Y}_i - \bar{Y})^2\).
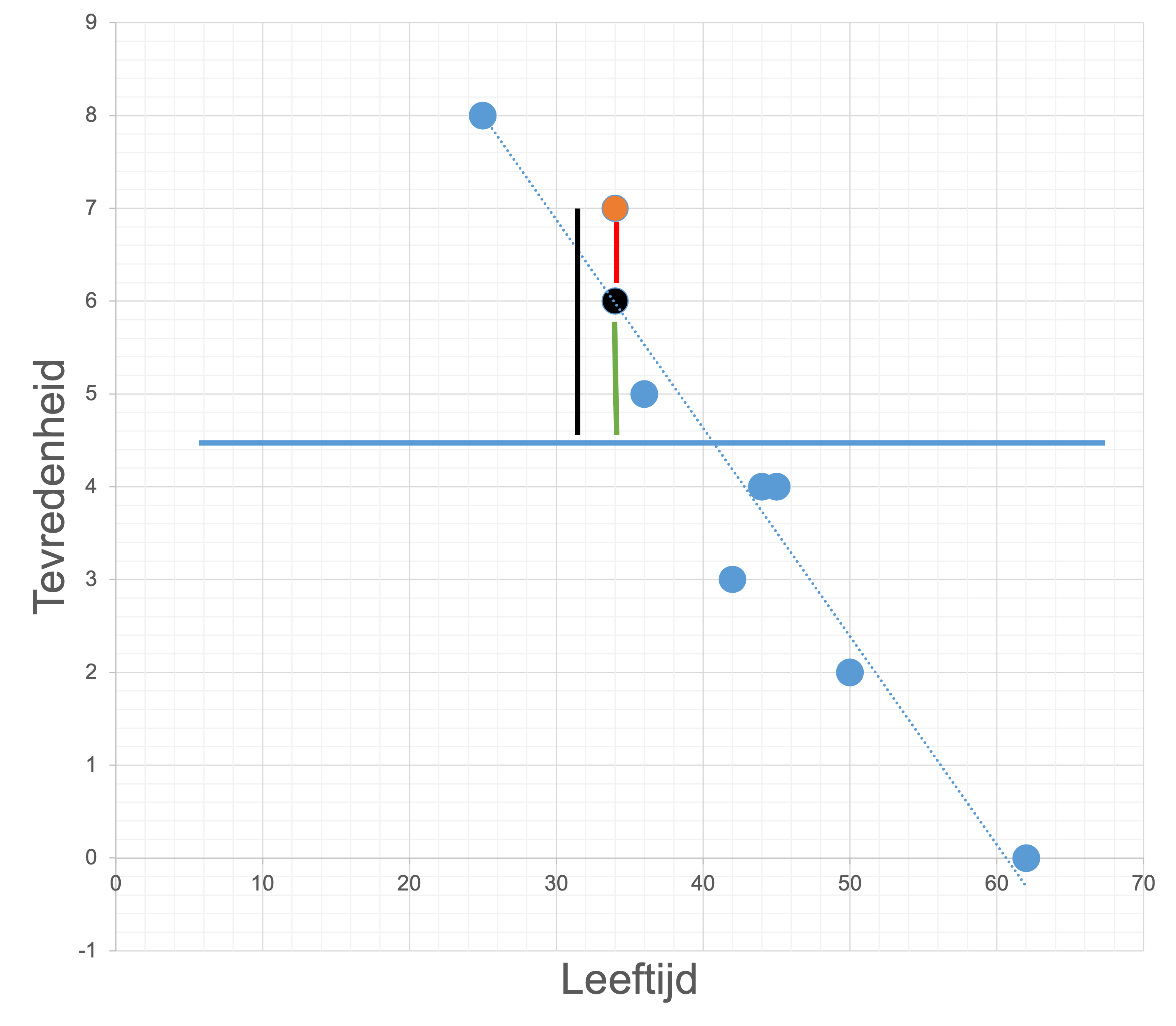
Figure 3.1: Grafische weergave van variantiebronnen
Uitgewerkt voor de oranje bol (\(X = 34, Y = 7\)) in figuur 3.1:
- SST: de afstand tussen de oranje bol \(Y_i\) en de blauwe horizontale lijn \(\bar{Y}\) ofwel \({Y}_i - \bar{Y} = 7 - 4,3 = 2,7\).
- SSE: de afstand tussen de oranje bol \(Y_i\) en de regressielijn \(\hat{Y}\) voor \(X = 34\) ofwel \({Y}_i - \hat{Y} = 7 - (13.6 + (-0.2) \times 34) = 7 - 6 = 1\). (opmerking: hier werden alle cijfers na de komma meegenomen, het volledige model is: \(\beta_0 = 13.6177\) en \(\beta_1 = -0.02246\)).
- SSR: de afstand tussen \(\hat{Y}\) en \(\bar{Y}\).
Wanneer we deze oefening voor alles observaties zouden herhalen en kwadrateren en optellen, komen we tot de uiteindelijke kwadratensom.
| SST | SSE | SSR |
|---|---|---|
| 3.6666667 | -0.0021598 | 3.6688265 |
| 1.6666667 | 0.0194384 | 1.6472282 |
| 2.6666667 | 1.0194384 | 1.6472282 |
| 0.6666667 | -0.5313175 | 1.1979842 |
| -1.3333333 | -1.1835853 | -0.1497480 |
| -0.3333333 | 0.2656587 | -0.5989921 |
| -0.3333333 | 0.4902808 | -0.8236141 |
| -2.3333333 | -0.3866091 | -1.9467243 |
| -4.3333333 | 0.3088553 | -4.6421886 |
Wanneer we al deze waarden kwadrateren komen we tot volgende tabel:
| SST | SSE | SSR |
|---|---|---|
| 13.4444444 | 0.0000047 | 13.4602878 |
| 2.7777778 | 0.0003779 | 2.7133608 |
| 7.1111111 | 1.0392547 | 2.7133608 |
| 0.4444444 | 0.2822983 | 1.4351661 |
| 1.7777778 | 1.4008742 | 0.0224245 |
| 0.1111111 | 0.0705746 | 0.3587915 |
| 0.1111111 | 0.2403752 | 0.6783402 |
| 5.4444444 | 0.1494666 | 3.7897354 |
| 18.7777778 | 0.0953916 | 21.5499152 |
Tot slot tellen we alles op:
| x | |
|---|---|
| SST | 50.000000 |
| SSE | 3.278618 |
| SSR | 46.721382 |
Zoals jullie kunnen opmerken uit de laatste tabel, geldt voor de variantiebronnen dat \(SST = SSE + SSR\).
Performantie van het regressiemodel
De performantie of verklarende kracht van het regressiemodel wordt uitgedrukt aan de hand van de determinatiecoëfficiënt (\(R^2\)). Deze geeft weer hoeveel van de variantie in \(Y\) verklaard kan worden aan de hand van één of meerdere onafhankelijke \(X\) variabelen. Meer bepaald is \(R^2 = \frac{SSR}{SST} = 1 - \frac{SSE}{SST}\). In het voorbeeld hierboven gegeven is \(R^2 = 0.93\) ofwel \(93%\). De determinatiecoëfficiënt varieerd tussen 0 en 1 (\(R^2 \in [0,1]\)) en hoe dichter bij \(1\), hoe meer van de variantie verklaard kan worden.
Deze berekening wijkt af van de slides door afronding. In de slides werd er geen afronding meegenomen, maar in dit boek werd dit wel meegenomen.
Een volledig overzicht van alle variantiebronnen is weergegeven in onderstaande tabel:
| Bron | Kwadratensom (SS) | Vrijheidsgraden (df) | Kwadratengemiddelde (MS) |
|---|---|---|---|
| Regressie | \(\sum ( \hat{Y}_i - \bar{Y})^2\) | \(m\) | \(\frac{\sum ( \hat{Y}_i - \bar{Y})^2}{m}\) |
| Residu/Fout | \(\sum ( Y_i - \hat{Y})^2\) | \(n-m-1\) | \(\frac{\sum ( Y_i - \hat{Y})^2}{n-m-1}\) |
| Totaal | \(\sum ( Y_i - \bar{Y})^2\) | \(n-1\) | \(\frac{\sum ( Y_i - \bar{Y})^2}{n-1}\) |
De uiteindelijke statistische grootheid op basis waarvan de uiteindelijke \(p\)-waarde berekend wordt, is gebaseerd op een afgeleide van de kwadratensom, namelijk het kwadratengemiddelde. Hiervoor wordt elke kwadratensom gedeeld door de bijhorende vrijheidsgraden. Deze vrijheidsgraden zijn \(n-1\) voor de SST (zoals in de formule van variantie uit eerste/tweede Bachelor), \(m\) voor de SSR (waarbij \(m\) het aantal onafhelijke variabelen weergeeft) en \(n-m-1\) voor de SSE. De F-statistiek wordt uiteindelijk berekend als \(F = MS_{regressie}/MS_{residu}\). Hoe groter de waarde van \(F\), hoe meer de regressie in staat is om variantie te verklaren en hoe sneller een statisch signifcant resultaat gevonden kan worden. Voor het tevreden voorbeeld is \(n-1 = 8\), \(m = 1\) en \(n-m-1 = 8-1-1 = 6\). Hieruit kunnen we \(F\) berekenen als \(F = \frac{46.7}{1}/\frac{3.3}{6} = 84.9\)
Figure 3.2: Grafische weergave van variantiebronnen
Op basis van de berekende \(F\)-waarde en de nul-distributie zoals weergegeven in figuur 3.2, zal de \(p\)-waarde \(< 0.001\). Het regressiemodel is met andere waaorden in staat om een significant deel van de variantie van \(Y\) te verklaren op basis van waarden van \(X\).
Bij uitbreiding naar meervoudige lineaire regressie wordt een model als volgt weergegeven: \(Y = \beta_0 + \beta_1X_1 + \beta_2X_2 + … + \epsilon\), waarbij \(Y\) de afhankelijke continue variabele is, \(X_i\) de onafhenkelijke variabele is, \(\beta_i\) een inschatting is van het verband tussen \(X_i\) en \(Y\) en \(\epsilon\) de fout is die gemaakt wordt door het model (\(Y_i - \hat{Y}_i\)).
Hypothesen
Binnen regressie kunnen er twee hypothesen worden opgesteld: (1) een hypothese over de regressie-analyse zelf en (2) een hypothese over de \(\beta\) coëfficiënten. De hypothese kunnen we algemeen als volgt opstellen:
- \(H_0\): Er is geen verband (\(\beta_i = 0\)) tussen de leeftijd (\(X_i\)) van de therapeut en de gegeven tevredenheidsscore (\(Y_i\)).
- \(H_1\): Er is een verband (\(\beta_i \neq 0\)) tussen de leeftijd (\(X_i\)) van de therapeut en de gegeven tevredenheidsscore (\(Y_i\)).
Een significante \(\beta_i\) wil dus zeggen significant verschillend van 0 en dus een meerwaarde om iets te zeggen over \(Y\). Let op: binnen deze hypothesen kan het ook over meervoudige regressie gaan met verschillende \(\beta\) coefficiënten.
\(H_0\) kan in dit geval \(\beta_1 = \beta_2 = \beta_3 = 0\) zijn.
Er wordt nooit een hypothese gevormd over \(\beta_0\). Kan je zelf bedenken waarom dit het geval is?