Meervoudige regressie

Een meervoudig lineair regressiemodel wordt weergegeven aan de hand van \(Y = \beta_0 + \beta_1X_1 + \beta_2X_2+...+\epsilon\). Binnen deze regressievergelijking kunnen we confounder opnemen en kunnen we ook interactie-effecten (moderatie) opnemen, maar geen mediatie.

Confounder

Een voorbeeld van de interpretatie van een regressiemodel wanneer we confounder opnemen is als volgt:

Meervoudige regressie: opnemen van meerdere factoren >> correctie van het effect voor de andere factoren.

\(Tevredenheid = \beta_0 + \beta_1 \times leeftijd + \beta_2 \times geslacht(man)\)

• \(\beta_1\) = inschatting van het effect van leeftijd op tevredenheid gecorrigeerd voor geslacht.
• \(\beta_2\) = inschatting van het effect van geslacht op tevredenheid gecorrigeerd voor leeftijd.

Moderatie

Bij een moderatie-analyse wordt er gebruik gemaakt van interacties. Een interactie wordt als volgt weergegeven in een regressievergelijking:

\(Y = \beta_0 + \beta_1 \times X_1 + \beta_2 \times X_2 + \beta_3 \times X_1 \times X_2 + \epsilon\)

\(\beta_3\) geeft in deze formule de interactie weer tussen \(X_1\) en \(X_2\). De interpretatie van \(\beta_3\) is echter moeilijk op basis van bovenstaande formule. WAnneer we deze formule herschrijven als

\(Y = \beta_0 + \beta_2 \times X_2 + (\beta_1 + \beta_3 \times X_1) \times X_2 + \epsilon\),

kunnen we heft effect van deze \(\beta_3\) beter evalueren. De associatie tussen \(Y\) en \(X_2\) wordt nu weergegeven door \((\beta_1 + \beta_3 \times X_1)\), waarbij de associatie:

• \(\beta_1 + \beta_3\) is wanneer \(X_1 = 1\)
• \(\beta_1\) is wanneer \(X_1 = 0\)

Stel dat \(Y = tevredenheid\), \(X_1 = leeftijd\) en \(X_2 = geslacht\). Wanneer er bij mannen een toename zou zijn in tevredenheid bij een stijgende leeftijd en bij vrouwen een afname in tevredenheid bij een stijgende leeftijd, dan is er een interactie-effect, waarbij \(\beta_3\) significant zal zijn.

Een visuele weergave van een interactie-effect is terug te vinden in figuur 5.7. Zwart geeft de associatie weer voor vrouwen, terwijl lichtgrijs de assocaitie weergeeft voor mannen.

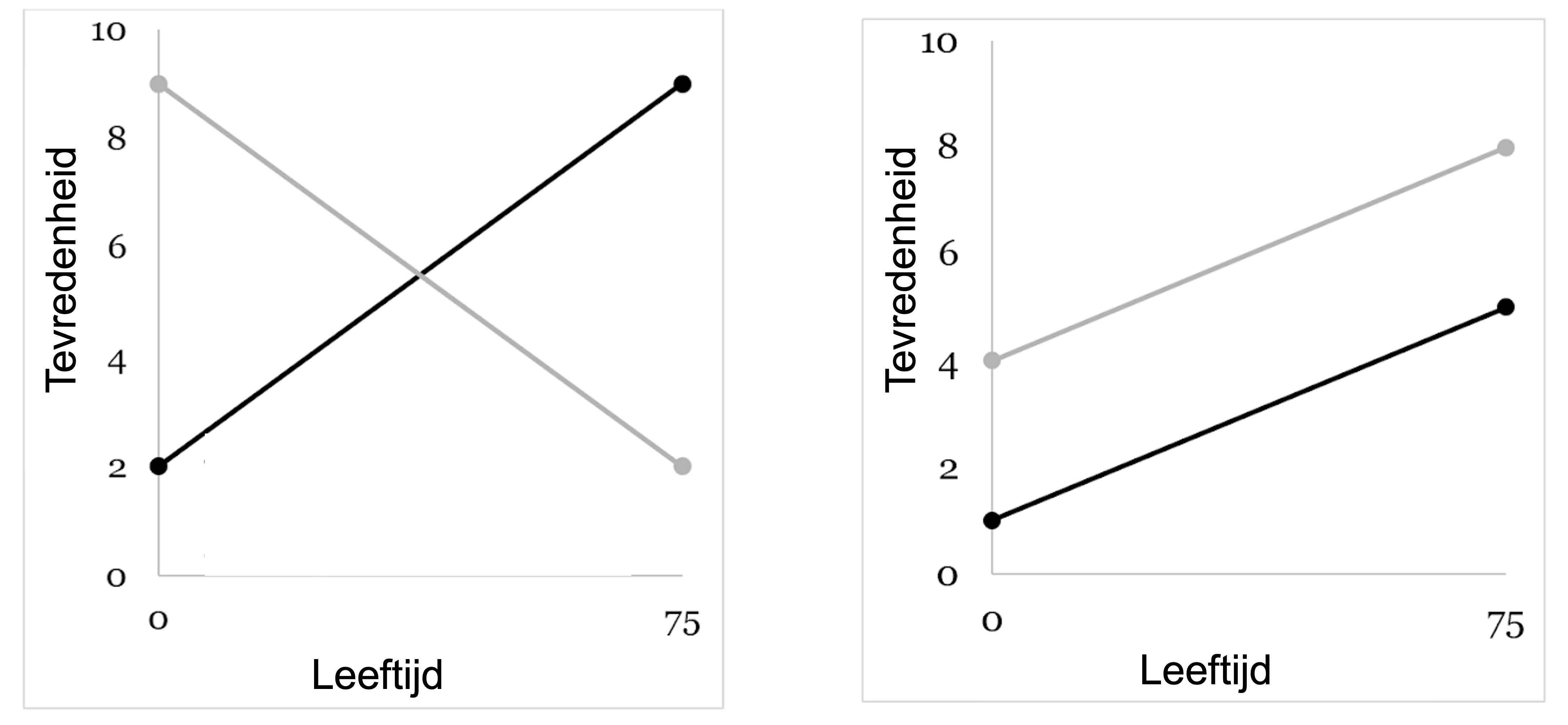
Figure 5.7: DAG

We kunnen intreactie of moderatie-effecten gebruiken voor alle combinaties van variabelen:

• categrosch x categorisch
• categorisch x continu
• continu x continu